Prioritized Experience Replay - DeepLearningを勉強する人

[1511.05952] Prioritized Experience Replay

論文まとめ

Online RLの問題点

遷移(transition)間の依存関係の影響が大きい
レアな遷移をすぐに捨ててしまう

そこで、

Experience Replay(ER)

DQNでは、replay mem.からランダムサンプリングしたミニバッチを使って更新する.
ERをより効率的、効果的にするには？？
優先順位を付けてサンプリングする.
より学習の進行が期待される遷移をより頻繁にリプレイするようにする.

ニューロサイエンス的な話

休憩している時や寝ている時に、海馬は過去の経験を"リプレイ"している.
特に、報酬に結びついている経験をより頻繁にリプレイしているらしい.
更に、"TD-error"の大きい経験もより頻繁にリプレイされるらしい.

Planningにおけるprioritization

planning(つまりmodel-freeではない)では、prioritizingが有効的であることが知られている.
Prioritized sweeping（更新した時の価値の変化に応じて優先度付けするような手法）

model-freeではTD-errorがこの優先度の基準に対応する尺度のひとつとなる. 更にここではstochastic prioritizationを行うことで、サンプルから関数近似を行う場合よりロバストになる.

Prioritized Replay

優先度を付けるには、以下の二つの方針があるが、今回は下の方

どの経験を格納するか？
どの経験をリプレイするか？

TD-errorによるprioritization

理想的な尺度→現在のステートにおいて、どの遷移からどの程度学習することができるか
これは直接的には分からないので、代わりに TD-error $\delta$ を用いる.
直感的には、どれだけ"驚いたか"、どれだけ予想していない遷移だったかを表し、bootstrappingした推定値と実測値がどの程度離れていたかを示す尺度.

greedy TD-error prioritization

最も単純な考え方で、TD-errorの絶対値が最大のものをリプレイする.
新しい遷移は、最低1回はサンプリングされることを保証するために最高の優先度で格納される.
メモリサイズを $N$ にスケールさせるために、優先度キューにはバイナリヒープを用いる.
そうするとサンプリングが $O(1)$ で、追加が $O(\log N)$ で可能.

stochastic prioritization

greedy TD-error prioritizationにはいくつか問題点がある.

リプレイされたTD-errorのみを更新するので、最初が低いTD-errorだと、長期間放置され得る
ノイズのスパイクに過剰反応してしまう（確率的な報酬の場合など）. 特にbootstrappingの場合だと、より顕著.
局所的な遷移(TD-error大きいものが頻繁にリプレイされる)しか見ないので学習が遅くなる. 多様性がなくなるので、overfittingの元となる.

確率的なサンプリングによって、uniform(通常のER)とgreedyの中間的なことをする.

どういう確率分布を考えるか？

優先度に関して単調
低い優先度でも非ゼロ

これを踏まえて、遷移 $i$ のサンプリング確率を以下で定義する.
${ \displaystyle P(i) = \frac {p_i^{\alpha}}{\sum_k p_k^{\alpha}} }$
$p_i > 0$ は遷移 $i$ の優先度、 $\alpha$ はどの程度優先度を重視するかに対応するハイパーパラメータ( $\alpha=0$ ならばuniform)

Proportional Prioritization ( direct )

$p_i = |\delta_i| + \epsilon$ , $\epsilon$ は小さい正定数でTD-errorが0になっても、それ以降サンプリングされないことを防ぐ.
( proportionalについては今回は割愛する )

Rank-based Prioritization ( indirect )

$\displaystyle p_i = \frac{1}{rank(i)}$ , $rank(i)$ は、遷移が $|\delta_i|$ に従ってリプレイメモリに格納された時の順位.
この場合、
${ \displaystyle P(i) = \frac { \biggl(\frac{1}{rank(i)} \biggr)^{\alpha}}{\sum_k \biggl(\frac{1}{rank(k)} \biggr)^{\alpha}} \\ = const. \biggl(\frac{1}{rank(i)} \biggr)^{\alpha} }$
となるので、 $P$ はスケーリング指数 $\alpha$ の冪乗則分布となる.
propotionalと比べて、外れ値に対して過剰反応しないのでよりロバスト性が期待できる（らしい）

サンプリングを効率化するには、計算コストは $N$ に依存してはならない.

累積分布関数を $k$ 個の等確率区間から成る区分線形関数で近似する. 区間の境界はあらかじめ計算される( $N$ と $\alpha$ に依存する)
区間をサンプリングする.
各区間からランダムサンプリングする.

ミニバッチベースの場合、 $k$ をミニバッチサイズに設定し、各区間から1遷移をサンプリングする.
これは、層状抽出法（stratified sampling）に対応する.
利点としては、バランスの取れたミニバッチが生成できる.

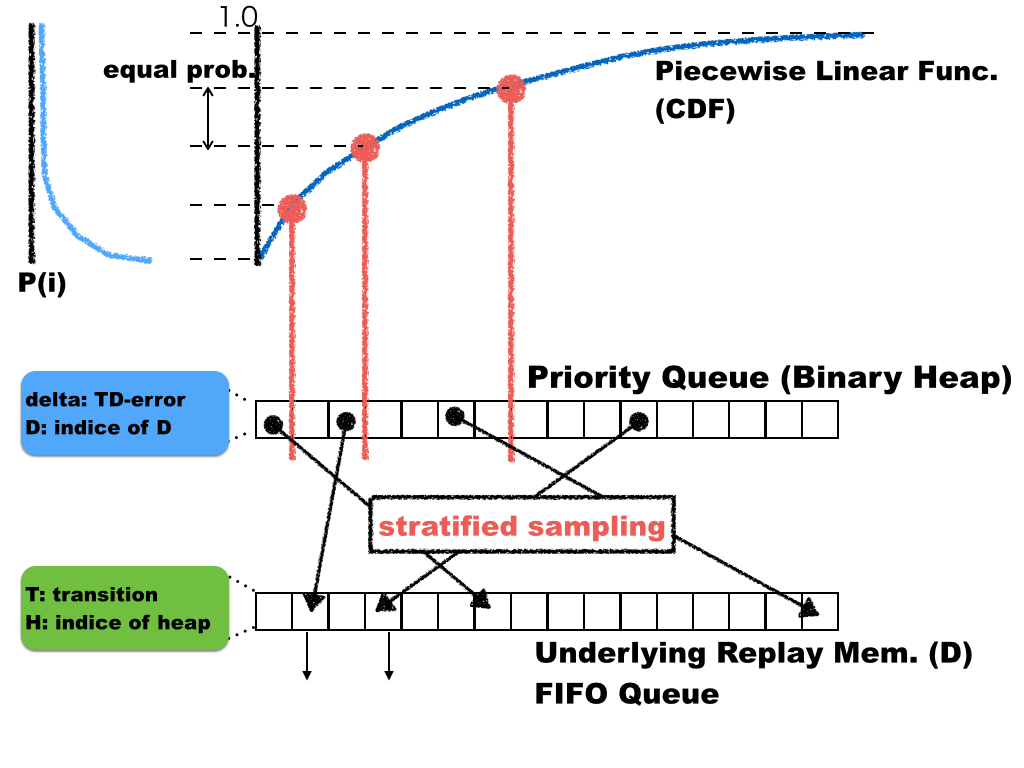
以下は、自分の実装方法も含めた全体の概略図.
f:id:wanwannodao:20170331180557p:plain

Annealing the bias

PRはこのサンプリングの分布を変化させるような"bias"を生じるので、確率的更新による期待値の推定値の収束する値も変わってしまう.
これをImportance Sampling(IS)によって修正する.
${\displaystyle w_i = \biggl( \frac{1}{N} \cdot \frac{1}{P(i)} \biggr)^{\beta} }$
（分子くる分布はは一様分布ということ？？）
${\beta=1}$ の場合、完全なISを行うことに対応する.
Q-learningの枠組みではTD-targetをこれで重み付けすればよく、 $\delta_i$ の代わりに $w_i\delta_i$ を用いる.
安定性の理由から、重みは $\frac{1}{`\max_i w_i}$ で正規化する.

指数 $\beta$ を学習の終了時に1に到達するようにスケジューリングする.　（更新にbiasがないことは収束する付近では重要な性質）
例えば、初期値 $\beta_0$ から線形的に1に近づける.
（アニーリングする理由は、full IS( ${\beta=1}$ )の場合重みが小さくなって初期の学習が遅くなるから？？）

配列ベースのバイナリヒープによる優先度付きキューを近似的にソートされた配列として使用する.
木が不均衡になりすぎないように, $10^6$ ステップ毎にソートしなおす.
(毎回完全にソートした配列を利用した場合と比較してあまり性能的な変化はなかった）
αとβはたまに更新する.
※
$\beta$ : とれだけbiasを修正するか
$\alpha$ : どれだけサンプリングの優先度を重要視するか

実装

github.com

データ構造

上図に示したように、一番下は通常のExperience Replayと同様に、リングバッファで管理する.
そのリングバッファ上のインデックスを管理して、Prioritized Replay を行う.

つまり、PRのバイナリヒープは対応するリングバッファのインデックスと、優先度付けのためのTD-errorの情報を持っている.
一方、リングバッファの方は対応するバイナリヒープのインデックスと、遷移の情報を持っている.

確率分布

dist = np.asarray([(1.0/(i+1))**self.alpha for i in range(n)], dtype=np.float32)

累積密度分布

cdf = np.cumsum(dist)

区間の計算

unit = (1.0 - cdf[0])/self.k
self.seg = [ np.searchsorted(cdf, cdf[0]+unit*i) for i in range(self.k) ]

アニーリング

self.beta += self.beta_step

サンプリングとIS weight

h_indices =[ np.random.randint(self.seg[i], self.seg[i+1]) \
               for i in range(self.k) ]
h = np.asarray(self.heap)[h_indices]
d_indices = [i['D'] for i in h]
d = np.asarray(self.D)[d_indices]
rank = np.asarray([ p['heap']+1 for p in d], dtype=np.int32)
is_w = ((rank**self.alpha) * self.p_n)** self.beta

return d, is_w

更新

max_is = tf.reduce_max(self.is_w)
self.loss = tf.reduce_mean( (self.is_w / max_is)  * self.delta)

結果

環境はOpenAI gymのMsPacman-v0
今回も時間とメモリの都合上完全な再現はできなかったが、
$\alpha=0.7$
$\beta=0.5 to 1.0$
メモリサイズ $50000$
$\epsilon = 1.0 to 0.01$ (1M step)
target net の更新は $30000$ step毎
ネットワークの構成は"Tuned" Double-DQN
で行った.
f:id:wanwannodao:20170331193114p:plain

右肩上がりの段階で止めてしまったのが惜しい.
追い追い、各手法を比較できればと思う.